how to find the 3rd side of a triangle

Triangle with at least 2 sides congruent

Isosceles triangle
Isosceles triangle with vertical centrality of symmetry
Blazon	triangle
Edges and vertices	3
Schläfli symbol	( ) ∨ { }
Symmetry group	Dih2, [ ], (*), social club ii
Properties	convex, cyclic

In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having exactly ii sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle every bit a special case. Examples of isosceles triangles include the isosceles correct triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.

The mathematical study of isosceles triangles dates dorsum to aboriginal Egyptian mathematics and Babylonian mathematics. Isosceles triangles have been used as ornamentation from even earlier times, and appear frequently in architecture and design, for case in the pediments and gables of buildings.

The two equal sides are called the legs and the third side is chosen the base of the triangle. The other dimensions of the triangle, such as its height, area, and perimeter, can be calculated by uncomplicated formulas from the lengths of the legs and base. Every isosceles triangle has an axis of symmetry along the perpendicular bisector of its base of operations. The two angles reverse the legs are equal and are always acute, so the nomenclature of the triangle as acute, correct, or obtuse depends only on the bending between its two legs.

Terminology, classification, and examples [edit]

Euclid divers an isosceles triangle as a triangle with exactly 2 equal sides,^[1] but modernistic treatments prefer to define isosceles triangles as having at least two equal sides. The difference between these two definitions is that the modern version makes equilateral triangles (with three equal sides) a special case of isosceles triangles.^[two] A triangle that is not isosceles (having iii unequal sides) is called scalene.^[three] "Isosceles" is made from the Greek roots "isos" (equal) and "skelos" (leg). The aforementioned word is used, for instance, for isosceles trapezoids, trapezoids with two equal sides,^[4] and for isosceles sets, sets of points every three of which form an isosceles triangle.^[5]

In an isosceles triangle that has exactly two equal sides, the equal sides are called legs and the third side is called the base of operations. The angle included by the legs is called the vertex angle and the angles that have the base as 1 of their sides are called the base of operations angles.^[vi] The vertex opposite the base is called the apex.^[7] In the equilateral triangle case, since all sides are equal, any side tin can exist chosen the base.^[eight]

A gilded triangle subdivided into a smaller golden triangle and golden gnomon

Whether an isosceles triangle is astute, right or birdbrained depends just on the bending at its apex. In Euclidean geometry, the base angles can not be obtuse (greater than xc°) or right (equal to 90°) because their measures would sum to at least 180°, the total of all angles in any Euclidean triangle.^[8] Since a triangle is obtuse or right if and only if one of its angles is obtuse or right, respectively, an isosceles triangle is obtuse, right or astute if and merely if its noon angle is respectively obtuse, right or acute.^[7] In Edwin Abbott'southward book Flatland, this classification of shapes was used as a satire of social hierarchy: isosceles triangles represented the working class, with acute isosceles triangles higher in the hierarchy than correct or obtuse isosceles triangles.^[9]

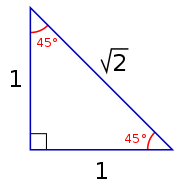
As well as the isosceles right triangle, several other specific shapes of isosceles triangles have been studied. These include the Calabi triangle (a triangle with three congruent inscribed squares),^[10] the golden triangle and golden gnomon (two isosceles triangles whose sides and base of operations are in the gilt ratio),^[eleven] the lxxx-80-20 triangle appearing in the Langley's Adventitious Angles puzzle,^[12] and the 30-thirty-120 triangle of the triakis triangular tiling. 5 Catalan solids, the triakis tetrahedron, triakis octahedron, tetrakis hexahedron, pentakis dodecahedron, and triakis icosahedron, each have isosceles-triangle faces, as do infinitely many pyramids^[viii] and bipyramids.^[13]

Formulas [edit]

Height [edit]

For any isosceles triangle, the post-obit six line segments coincide:

• the altitude, a line segment from the apex perpendicular to the base,^[14]
• the angle bisector from the apex to the base of operations,^[fourteen]
• the median from the apex to the midpoint of the base,^[14]
• the perpendicular bisector of the base within the triangle,^[fourteen]
• the segment within the triangle of the unique axis of symmetry of the triangle, and^[xiv]
• the segment within the triangle of the Euler line of the triangle, except when the triangle is equilateral.^[15]

Their common length is the meridian ${\displaystyle h}$ of the triangle. If the triangle has equal sides of length ${\displaystyle a}$ and base of length ${\displaystyle b}$ , the general triangle formulas for the lengths of these segments all simplify to^[16]

${\displaystyle h={\sqrt {a^{two}-{\frac {b^{ii}}{four}}}}.}$

This formula tin also be derived from the Pythagorean theorem using the fact that the distance bisects the base and partitions the isosceles triangle into 2 coinciding right triangles.^[17]

The Euler line of whatever triangle goes through the triangle's orthocenter (the intersection of its three altitudes), its centroid (the intersection of its three medians), and its circumcenter (the intersection of the perpendicular bisectors of its three sides, which is also the center of the circumcircle that passes through the three vertices). In an isosceles triangle with exactly 2 equal sides, these 3 points are distinct, and (by symmetry) all lie on the symmetry axis of the triangle, from which it follows that the Euler line coincides with the axis of symmetry. The incenter of the triangle besides lies on the Euler line, something that is not true for other triangles.^[15] If any two of an angle bisector, median, or altitude coincide in a given triangle, that triangle must exist isosceles.^[xviii]

Area [edit]

The expanse ${\displaystyle T}$ of an isosceles triangle can be derived from the formula for its height, and from the general formula for the expanse of a triangle as one-half the product of base and superlative:^[16]

${\displaystyle T={\frac {b}{4}}{\sqrt {4a^{2}-b^{two}}}.}$

The same area formula can also be derived from Heron'due south formula for the area of a triangle from its three sides. All the same, applying Heron's formula directly tin can exist numerically unstable for isosceles triangles with very precipitous angles, because of the about-cancellation between the semiperimeter and side length in those triangles.^[19]

If the noon angle ${\displaystyle (\theta )}$ and leg lengths ${\displaystyle (a)}$ of an isosceles triangle are known, then the area of that triangle is:^[xx]

${\displaystyle T={\frac {1}{2}}a^{2}\sin \theta .}$

This is a special case of the full general formula for the area of a triangle as one-half the product of two sides times the sine of the included angle.^[21]

Perimeter [edit]

The perimeter ${\displaystyle p}$ of an isosceles triangle with equal sides ${\displaystyle a}$ and base ${\displaystyle b}$ is just^[sixteen]

${\displaystyle p=2a+b.}$

As in whatever triangle, the area ${\displaystyle T}$ and perimeter ${\displaystyle p}$ are related by the isoperimetric inequality^[22]

${\displaystyle p^{2}>12{\sqrt {3}}T.}$

This is a strict inequality for isosceles triangles with sides unequal to the base, and becomes an equality for the equilateral triangle. The area, perimeter, and base of operations can also be related to each other past the equation^[23]

${\displaystyle 2pb^{3}-p^{ii}b^{2}+16T^{2}=0.}$

If the base and perimeter are fixed, then this formula determines the area of the resulting isosceles triangle, which is the maximum possible among all triangles with the same base of operations and perimeter.^[24] On the other hand, if the expanse and perimeter are fixed, this formula can be used to recover the base length, simply not uniquely: in that location are in general two distinct isosceles triangles with given expanse ${\displaystyle T}$ and perimeter ${\displaystyle p}$ . When the isoperimetric inequality becomes an equality, there is only one such triangle, which is equilateral.^[25]

Angle bisector length [edit]

If the ii equal sides accept length ${\displaystyle a}$ and the other side has length ${\displaystyle b}$ , and so the internal angle bisector ${\displaystyle t}$ from ane of the two equal-angled vertices satisfies^[26]

${\displaystyle {\frac {2ab}{a+b}}>t>{\frac {ab{\sqrt {2}}}{a+b}}}$

as well every bit

${\displaystyle t<{\frac {4a}{3}};}$

and conversely, if the latter condition holds, an isosceles triangle parametrized by ${\displaystyle a}$ and ${\displaystyle t}$ exists.^[27]

The Steiner–Lehmus theorem states that every triangle with two angle bisectors of equal lengths is isosceles. Information technology was formulated in 1840 by C. 50. Lehmus. Its other namesake, Jakob Steiner, was one of the kickoff to provide a solution.^[28] Although originally formulated simply for internal bending bisectors, it works for many (but not all) cases when, instead, two external bending bisectors are equal. The 30-30-120 isosceles triangle makes a purlieus case for this variation of the theorem, every bit it has iv equal angle bisectors (two internal, two external).^[29]

Radii [edit]

Isosceles triangle showing its circumcenter (blue), centroid (cherry), incenter (green), and symmetry axis (purple)

The inradius and circumradius formulas for an isosceles triangle may exist derived from their formulas for arbitrary triangles.^[30] The radius of the inscribed circle of an isosceles triangle with side length ${\displaystyle a}$ , base of operations ${\displaystyle b}$ , and height ${\displaystyle h}$ is:^[16]

${\displaystyle {\frac {2ab-b^{2}}{4h}}.}$

The eye of the circle lies on the symmetry centrality of the triangle, this distance above the base. An isosceles triangle has the largest possible inscribed circle amid the triangles with the aforementioned base and apex angle, besides as also having the largest area and perimeter among the same class of triangles.^[31]

The radius of the circumscribed circumvolve is:^[16]

${\displaystyle {\frac {a^{2}}{2h}}.}$

The heart of the circle lies on the symmetry axis of the triangle, this distance below the apex.

Inscribed square [edit]

For any isosceles triangle, there is a unique square with one side collinear with the base of the triangle and the opposite ii corners on its sides. The Calabi triangle is a special isosceles triangle with the holding that the other two inscribed squares, with sides collinear with the sides of the triangle, are of the aforementioned size as the base square.^[10] A much older theorem, preserved in the works of Hero of Alexandria, states that, for an isosceles triangle with base ${\displaystyle b}$ and meridian ${\displaystyle h}$ , the side length of the inscribed square on the base of the triangle is^[32]

${\displaystyle {\frac {bh}{b+h}}.}$

Isosceles subdivision of other shapes [edit]

Partitioning of a cyclic pentagon into isosceles triangles by radii of its circumcircle

For any integer ${\displaystyle north\geq four}$ , whatever triangle tin exist partitioned into ${\displaystyle n}$ isosceles triangles.^[33] In a right triangle, the median from the hypotenuse (that is, the line segment from the midpoint of the hypotenuse to the right-angled vertex) divides the right triangle into ii isosceles triangles. This is considering the midpoint of the hypotenuse is the center of the circumcircle of the right triangle, and each of the two triangles created by the sectionalization has two equal radii as ii of its sides.^[34] Similarly, an acute triangle can be partitioned into three isosceles triangles past segments from its circumcenter,^[35] but this method does not work for obtuse triangles, because the circumcenter lies outside the triangle.^[30]

Generalizing the segmentation of an acute triangle, any cyclic polygon that contains the heart of its circumscribed circle can be partitioned into isosceles triangles by the radii of this circle through its vertices. The fact that all radii of a circle take equal length implies that all of these triangles are isosceles. This partition can be used to derive a formula for the area of the polygon as a function of its side lengths, even for cyclic polygons that exercise not contain their circumcenters. This formula generalizes Heron'south formula for triangles and Brahmagupta'south formula for cyclic quadrilaterals.^[36]

Either diagonal of a rhombus divides it into ii congruent isosceles triangles. Similarly, 1 of the two diagonals of a kite divides it into two isosceles triangles, which are not congruent except when the kite is a rhomb.^[37]

Applications [edit]

In compages and design [edit]

Isosceles triangles ordinarily appear in architecture as the shapes of gables and pediments. In aboriginal Greek architecture and its later imitations, the obtuse isosceles triangle was used; in Gothic architecture this was replaced by the astute isosceles triangle.^[8]

In the architecture of the Middle Ages, some other isosceles triangle shape became pop: the Egyptian isosceles triangle. This is an isosceles triangle that is acute, but less so than the equilateral triangle; its height is proportional to 5/eight of its base.^[38] The Egyptian isosceles triangle was brought back into utilise in modern architecture by Dutch architect Hendrik Petrus Berlage.^[39]

Warren truss structures, such as bridges, are ordinarily bundled in isosceles triangles, although sometimes vertical beams are also included for boosted strength.^[twoscore] Surfaces tessellated by obtuse isosceles triangles tin exist used to form deployable structures that have two stable states: an unfolded state in which the surface expands to a cylindrical column, and a folded state in which it folds into a more compact prism shape that can exist more easily transported.^[41] The aforementioned tessellation pattern forms the ground of Yoshimura buckling, a pattern formed when cylindrical surfaces are axially compressed,^[42] and of the Schwarz lantern, an example used in mathematics to show that the expanse of a smooth surface cannot ever be accurately approximated past polyhedra converging to the surface.^[43]

In graphic design and the decorative arts, isosceles triangles take been a frequent design element in cultures around the world from at least the Early Neolithic^[44] to modernistic times.^[45] They are a common design element in flags and heraldry, appearing prominently with a vertical base, for case, in the flag of Guyana, or with a horizontal base in the flag of Saint Lucia, where they form a stylized image of a mountain island.^[46]

They also have been used in designs with religious or mystic significance, for example in the Sri Yantra of Hindu meditational practice.^[47]

In other areas of mathematics [edit]

If a cubic equation with real coefficients has three roots that are non all real numbers, and so when these roots are plotted in the circuitous plane as an Argand diagram they form vertices of an isosceles triangle whose axis of symmetry coincides with the horizontal (real) axis. This is because the circuitous roots are complex conjugates and hence are symmetric about the real centrality.^[48]

In celestial mechanics, the 3-trunk problem has been studied in the special case that the iii bodies grade an isosceles triangle, because assuming that the bodies are arranged in this way reduces the number of degrees of liberty of the arrangement without reducing it to the solved Lagrangian point case when the bodies form an equilateral triangle. The outset instances of the three-body problem shown to have unbounded oscillations were in the isosceles three-body problem.^[49]

History and fallacies [edit]

Long before isosceles triangles were studied by the ancient Greek mathematicians, the practitioners of Ancient Egyptian mathematics and Babylonian mathematics knew how to calculate their area. Problems of this type are included in the Moscow Mathematical Papyrus and Rhind Mathematical Papyrus.^[50]

The theorem that the base angles of an isosceles triangle are equal appears as Suggestion I.5 in Euclid.^[51] This effect has been chosen the pons asinorum (the bridge of asses) or the isosceles triangle theorem. Rival explanations for this proper noun include the theory that it is because the diagram used by Euclid in his demonstration of the result resembles a bridge, or considering this is the kickoff difficult result in Euclid, and acts to divide those who can understand Euclid'due south geometry from those who cannot.^[52]

A well-known fallacy is the fake proof of the statement that all triangles are isosceles. Robin Wilson credits this argument to Lewis Carroll,^[53] who published it in 1899, but Due west. W. Rouse Ball published it in 1892 and later wrote that Carroll obtained the statement from him.^[54] The fallacy is rooted in Euclid's lack of recognition of the concept of betweenness and the resulting ambiguity of inside versus exterior of figures.^[55]

Notes [edit]

1. ^ Heath (1956), p. 187, Definition 20.
2. ^ Stahl (2003), p. 37.
3. ^ Usiskin & Griffin (2008), p. 4.
4. ^ Usiskin & Griffin (2008), p. 41.
5. ^ Ionin (2009).
6. ^ Jacobs (1974), p. 144.
7. ^ ^{a b} Gottschau, Haverkort & Matzke (2018).
8. ^ ^{a b c d} Lardner (1840), p. 46.
9. ^ Barnes (2012).
10. ^ ^{a b} Conway & Guy (1996).
11. ^ Loeb (1992).
12. ^ Langley (1922).
13. ^ Montroll (2009).
14. ^ ^{a b c d due east} Hadamard (2008), p. 23.
15. ^ ^{a b} Guinand (1984).
16. ^ ^{a b c d e} Harris & Stöcker (1998), p. 78.
17. ^ Salvadori & Wright (1998).
18. ^ Hadamard (2008), Do 5, p. 29.
19. ^ Kahan (2014).
20. ^ Immature (2011), p. 298.
21. ^ Young (2011), p. 398.
22. ^ Alsina & Nelsen (2009), p. 71.
23. ^ Baloglou & Helfgott (2008), Equation (1).
24. ^ Wickelgren (2012).
25. ^ Baloglou & Helfgott (2008), Theorem 2.
26. ^ Arslanagić.
27. ^ Oxman (2005).
28. ^ Gilbert & MacDonnell (1963).
29. ^ Conway & Ryba (2014).
30. ^ ^{a b} Harris & Stöcker (1998), p. 75.
31. ^ Alsina & Nelsen (2009), p. 67.
32. ^ Gandz (1940).
33. ^ Lord (1982). See also Hadamard (2008, Do 340, p. 270).
34. ^ Posamentier & Lehmann (2012), p. 24.
35. ^ Bezdek & Bisztriczky (2015).
36. ^ Robbins (1995).
37. ^ Usiskin & Griffin (2008), p. 51.
38. ^ Lavedan (1947).
39. ^ Padovan (2002).
40. ^ Ketchum (1920).
41. ^ Pellegrino (2002).
42. ^ Yoshimura (1955).
43. ^ Schwarz (1890).
44. ^ Washburn (1984).
45. ^ Jakway (1922).
46. ^ Smith (2014).
47. ^ Bolton, Nicol & Macleod (1977).
48. ^ Bardell (2016).
49. ^ Diacu & Holmes (1999).
50. ^ Høyrup (2008). Although "many of the early Egyptologists" believed that the Egyptians used an inexact formula for the expanse, half the product of the base and side, Vasily Vasilievich Struve championed the view that they used the right formula, half the product of the base and height (Clagett 1989). This question rests on the translation of 1 of the words in the Rhind papyrus, and with this word translated as height (or more precisely as the ratio of meridian to base of operations) the formula is right (Gunn & Peet 1929, pp. 173–174).
51. ^ Heath (1956), p. 251.
52. ^ Venema (2006), p. 89.
53. ^ Wilson (2008).
54. ^ Ball & Coxeter (1987).
55. ^ Specht et al. (2015).

References [edit]

• Alsina, Claudi; Nelsen, Roger B. (2009), When less is more than: Visualizing basic inequalities, The Dolciani Mathematical Expositions, vol. 36, Mathematical Association of America, Washington, DC, ISBN978-0-88385-342-ix, MR 2498836
• Arslanagić, Šefket, "Trouble η44", Inequalities proposed in Crux Mathematicorum (PDF), p. 151
• Brawl, W. W. Rouse; Coxeter, H. Due south. Thou. (1987) [1892], Mathematical Recreations and Essays (13th ed.), Dover, footnote, p. 77, ISBN0-486-25357-0
• Baloglou, George; Helfgott, Michel (2008), "Angles, surface area, and perimeter caught in a cubic" (PDF), Forum Geometricorum, 8: 13–25, MR 2373294
• Bardell, Nicholas S. (2016), "Cubic polynomials with real or complex coefficients: The full movie" (PDF), Australian Senior Mathematics Journal, 30 (2): 5–26
• Barnes, John (2012), Gems of Geometry (2d, illustrated ed.), Springer, p. 27, ISBN9783642309649
• Bezdek, András; Bisztriczky, Ted (2015), "Finding equal-diameter triangulations in polygons", Beiträge zur Algebra und Geometrie, 56 (two): 541–549, doi:ten.1007/s13366-014-0206-6, MR 3391189, S2CID 123507725
• Bolton, Nicholas J; Nicol, D.; Macleod, M. (March 1977), "The geometry of the Śrī-yantra", Religion, 7 (1): 66–85, doi:10.1016/0048-721x(77)90008-2
• Clagett, Marshall (1989), Ancient Egyptian Science: Ancient Egyptian mathematics, American Philosophical Society, Footnote 68, pp. 195–197, ISBN9780871692320
• Conway, J.H.; Guy, R.K. (1996), "Calabi's Triangle", The Book of Numbers, New York: Springer-Verlag, p. 206
• Conway, John; Ryba, Alex (July 2014), "The Steiner–Lehmus angle-bisector theorem", The Mathematical Gazette, 98 (542): 193–203, doi:x.1017/s0025557200001236, S2CID 124753764
• Diacu, Florin; Holmes, Philip (1999), Celestial Encounters: The Origins of Chaos and Stability, Princeton Science Library, Princeton Academy Press, p. 122, ISBN9780691005454
• Gandz, Solomon (1940), "Studies in Babylonian mathematics. III. Isoperimetric problems and the origin of the quadratic equations", Isis, 32: 101–115 (1947), doi:ten.1086/347645, MR 0017683, S2CID 120267556 . See in particular p. 111.
• Gilbert, G.; MacDonnell, D. (1963), "The Steiner–Lehmus Theorem", Classroom Notes, American Mathematical Monthly, lxx (ane): 79–80, doi:ten.2307/2312796, JSTOR 2312796, MR 1531983
• Gottschau, Marinus; Haverkort, Herman; Matzke, Kilian (2018), "Reptilings and infinite-filling curves for astute triangles", Discrete & Computational Geometry, threescore (1): 170–199, arXiv:1603.01382, doi:10.1007/s00454-017-9953-0, S2CID 14477196
• Guinand, Andrew P. (1984), "Euler lines, tritangent centers, and their triangles", American Mathematical Monthly, 91 (5): 290–300, doi:10.2307/2322671, JSTOR 2322671, MR 0740243
• Gunn, Battiscombe; Peet, T. Eric (May 1929), "Four geometrical problems from the Moscow Mathematical Papyrus", The Journal of Egyptian Archaeology, xv (1): 167–185, doi:ten.1177/030751332901500130, JSTOR 3854111, S2CID 192278129
• Hadamard, Jacques (2008), Lessons in Geometry: Plane geometry, translated by Saul, Mark, American Mathematical Lodge, ISBN9780821843673
• Harris, John Due west.; Stöcker, Horst (1998), Handbook of mathematics and computational science, New York: Springer-Verlag, doi:x.1007/978-1-4612-5317-4, ISBN0-387-94746-ix, MR 1621531
• Heath, Thomas L. (1956) [1925], The Xiii Books of Euclid's Elements, vol. 1 (2nd ed.), New York: Dover Publications, ISBN0-486-60088-2
• Høyrup, Jens (2008), "Geometry in Mesopotamia and Egypt", Encyclopaedia of the History of Scientific discipline, Technology, and Medicine in Non-Western Cultures, Springer Netherlands, pp. 1019–1023, Bibcode:2008ehst.volume.....S, doi:x.1007/978-1-4020-4425-0_8619
• Ionin, Yury J. (2009), "Isosceles sets", Electronic Periodical of Combinatorics, 16 (1): R141:1–R141:24, doi:10.37236/230, MR 2577309
• Jacobs, Harold R. (1974), Geometry, W. H. Freeman and Co., ISBN0-7167-0456-0
• Jakway, Bernard C. (1922), The Principles of Interior Decoration, Macmillan, p. 48
• Kahan, W. (September 4, 2014), "Miscalculating Area and Angles of a Needle-like Triangle" (PDF), Lecture Notes for Introductory Numerical Analysis Classes, University of California, Berkeley
• Ketchum, Milo Smith (1920), The Design of Highway Bridges of Steel, Timber and Physical, New York: McGraw-Hill, p. 107
• Langley, Eastward. M. (1922), "Problem 644", The Mathematical Gazette, 11: 173
• Lardner, Dionysius (1840), A Treatise on Geometry and Its Application in the Arts, The Cabinet Cyclopædia, London
• Lavedan, Pierre (1947), French Architecture, Penguin Books, p. 44
• Loeb, Arthur (1992), Concepts and Images: Visual Mathematics, Boston: Birkhäuser Boston, p. 180, ISBN0-8176-3620-Ten
• Lord, N. J. (June 1982), "66.16 Isosceles subdivisions of triangles", The Mathematical Gazette, 66 (436): 136–137, doi:10.2307/3617750, JSTOR 3617750
• Montroll, John (2009), Origami Polyhedra Blueprint, A M Peters, p. 6, ISBN9781439871065
• Oxman, Victor (2005), "On the existence of triangles with given lengths of 1 side, the reverse and ane side by side bending bisectors" (PDF), Forum Geometricorum, 5: 21–22, MR 2141652
• Padovan, Richard (2002), Towards Universality: Le Corbusier, Mies, and De Stijl, Psychology Press, p. 128, ISBN9780415259620
• Pellegrino, S. (2002), Deployable Structures, CISM International Eye for Mechanical Sciences, vol. 412, Springer, pp. 99–100, ISBN9783211836859
• Posamentier, Alfred S.; Lehmann, Ingmar (2012), The Secrets of Triangles: A Mathematical Journey, Amherst, NY: Prometheus Books, p. 387, ISBN978-one-61614-587-iii, MR 2963520
• Robbins, David P. (1995), "Areas of polygons inscribed in a circle", American Mathematical Monthly, 102 (6): 523–530, doi:x.2307/2974766, JSTOR 2974766, MR 1336638
• Salvadori, Mario; Wright, Joseph P. (1998), Math Games for Eye School: Challenges and Skill-Builders for Students at Every Level, Chicago Review Press, pp. lxx–71, ISBN9781569767276
• Schwarz, H. A. (1890), Gesammelte Mathematische Abhandlungen von H. A. Schwarz, Verlag von Julius Springer, pp. 309–311
• Smith, Whitney (June 26, 2014), "Flag of Saint Lucia", Encyclopædia Britannica , retrieved 2018-09-12
• Specht, Edward John; Jones, Harold Trainer; Calkins, Keith G.; Rhoads, Donald H. (2015), Euclidean geometry and its subgeometries, Springer, Cham, p. 64, doi:10.1007/978-3-319-23775-half-dozen, ISBN978-three-319-23774-9, MR 3445044
• Stahl, Saul (2003), Geometry from Euclid to Knots, Prentice-Hall, ISBN0-xiii-032927-4
• Usiskin, Zalman; Griffin, Jennifer (2008), The Classification of Quadrilaterals: A Study in Definition, Research in Mathematics Didactics, Data Age Publishing, ISBN9781607526001
• Venema, Gerard A. (2006), Foundations of Geometry, Prentice-Hall, ISBN0-thirteen-143700-3
• Washburn, Dorothy K. (July 1984), "A report of the red on cream and cream on ruby designs on Early on Neolithic ceramics from Nea Nikomedeia", American Periodical of Archeology, 88 (3): 305–324, doi:10.2307/504554, JSTOR 504554, S2CID 191374019
• Wickelgren, Wayne A. (2012), How to Solve Mathematical Problems, Dover Books on Mathematics, Courier Corporation, pp. 222–224, ISBN9780486152684 .
• Wilson, Robin (2008), Lewis Carroll in Numberland: His fantastical mathematical logical life, an desperation in eight fits, Penguin Books, pp. 169–170, ISBN978-0-14-101610-viii, MR 2455534
• Yoshimura, Yoshimaru (July 1955), On the mechanism of buckling of a circular cylindrical shell under axial compression, Technical Memorandum 1390, National Advisory Committee for Aeronautics
• Young, Cynthia Y. (2011), Trigonometry, John Wiley & Sons, ISBN9780470648025

External links [edit]

• Weisstein, Eric W., "Isosceles triangle", MathWorld

Source: https://en.wikipedia.org/wiki/Isosceles_triangle

Posted by: coatesperis1986.blogspot.com

Share this post