How To Find Local Max And Min From Graph Of Derivative

All local maximums and minimums on a function'south graph — called local extrema — occur at disquisitional points of the function (where the derivative is zip or undefined). Don't forget, though, that non all critical points are necessarily local extrema.

The get-go footstep in finding a function's local extrema is to detect its critical numbers (the x-values of the disquisitional points). You lot then use the Commencement Derivative Test. This test is based on the Nobel-prize-caliber ideas that as yous get over the peak of a hill, first you lot become upwardly and then you become downwards, and that when yous bulldoze into and out of a valley, yous go down and so up. This calculus stuff is pretty amazing, eh?

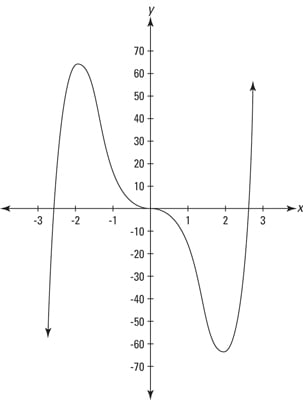
The figure shows the graph of

To detect the critical numbers of this function, here's what you do:

Observe the showtime derivative of f using the power rule.
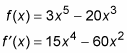
Set the derivative equal to zip and solve for 10.

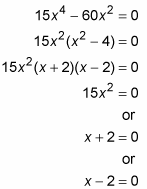
10 = 0, –ii, or 2.

These three x-values are the disquisitional numbers of f. Additional critical numbers could be if the first derivative were undefined at some 10-values, simply because the derivative

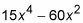
is defined for all input values, the above solution gear up, 0, –2, and 2, is the complete list of critical numbers. Because the derivative (and the slope) of f equals zero at these three disquisitional numbers, the curve has horizontal tangents at these numbers.

At present that you lot've got the listing of disquisitional numbers, you need to determine whether peaks or valleys or neither occur at those x-values. You tin can do this with the Start Derivative Test. Here's how:

Have a number line and put down the critical numbers y'all take found: 0, –2, and 2.

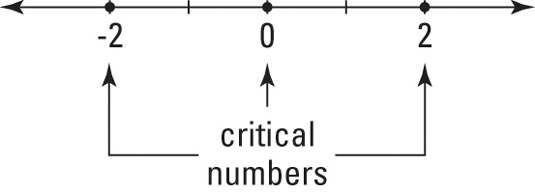
You divide this number line into four regions: to the left of –2, from –ii to 0, from 0 to 2, and to the correct of ii.
Option a value from each region, plug it into the first derivative, and notation whether your result is positive or negative.

For this example, you can use the numbers –three, –1, ane, and 3 to test the regions.

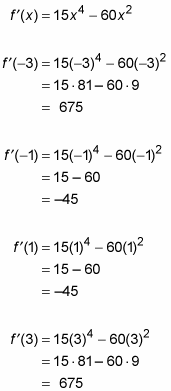
These iv results are, respectively, positive, negative, negative, and positive.
Have your number line, mark each region with the appropriate positive or negative sign, and indicate where the office is increasing and decreasing.

It's increasing where the derivative is positive, and decreasing where the derivative is negative. The consequence is a so-called sign graph for the function.

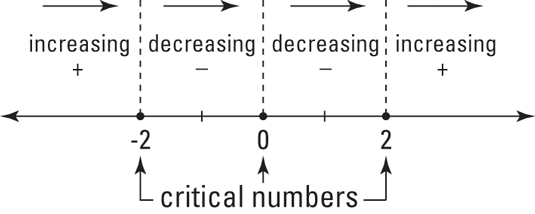
This figure simply tells yous what you lot already know if you've looked at the graph of f — that the part goes upwards until –2, down from –2 to 0, farther downwardly from 0 to 2, and up again from 2 on.

Now, here'southward the rocket science. The part switches from increasing to decreasing at –2; in other words, you go upwardly to –ii and then down. Then, at –2, you have a hill or a local maximum. Conversely, considering the role switches from decreasing to increasing at 2, you take a valley there or a local minimum. And because the sign of the first derivative doesn't switch at zero, there's neither a min nor a max at that x-value.
Obtain the function values (in other words, the heights) of these 2 local extrema by plugging the 10-values into the original part.

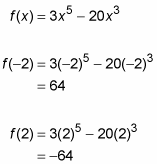
Thus, the local max is located at (–2, 64), and the local min is at (2, –64). Yous're done.

To utilize the Get-go Derivative Examination to test for a local extremum at a particular critical number, the role must be continuous at that ten-value.