How To Find The Mad Of A Dot Plot

43.4: Using Hateful and MAD to Brand Comparisons

1. Final updated

2. Relieve as PDF

Page ID

40875

Lesson

Allow's apply mean and MAD to describe and compare distributions.

Exercise \(\PageIndex{1}\): Number Talk: Decimal Division

Detect the value of each expression mentally.

\(42\div 12\)

\(2.4\div 12\)

\(44.4\div 12\)

\(46.8\div 12\)

Exercise \(\PageIndex{two}\): Which Player Would You Choose?

1. Andre and Noah joined Elena, Jada, and Lin in recording their basketball scores. They all recorded their scores in the same way: the number of baskets fabricated out of 10 attempts. Each nerveless 12 data points.
   • Andre's mean number of baskets was five.25, and his MAD was 2.vi.
   • Noah's hateful number of baskets was also 5.25, but his MAD was 1.

Hither are two dot plots that represent the two data sets. The triangle indicates the location of the mean.

Effigy \(\PageIndex{1}\): Two dot plots, number of baskets made, 0 to x by ones. Data set up A, beginning at 3, number of dots above each increase is ane, 2, 5, 2, 1, 1, triangle approximately 5 indicate ii. Data fix B, start at 1, number of dots above each increment is 1, 2, 1, 2, 0, 1, 1, 2, 2, triangle approximately 5 bespeak two.

1. Without computing, make up one's mind which dot plot represents Andre'southward data and which represents Noah'southward. Explain how you know.
2. If you were the captain of a basketball team and could employ one more than player on your team, would you choose Andre or Noah? Explicate your reasoning.

2. An eighth-grade pupil decided to join Andre and Noah and kept track of his scores. His data prepare is shown hither. The mean number of baskets he fabricated is 6.

Table \(\PageIndex{one}\)

eighth-class educatee	\(six\)	\(five\)	\(four\)	\(7\)	\(half dozen\)	\(v\)	\(seven\)	\(viii\)	\(5\)	\(six\)	\(five\)	\(eight\)
distance from \(6\)

1. Calculate the MAD. Testify your reasoning.
2. Describe a dot plot to represent his data and mark the location of the mean with a triangle (\(\Delta\)).
3. Compare the eighth-course student's mean and MAD to Noah's mean and MAD. What practise you find?
4. Compare their dot plots. What practise you notice virtually the distributions?
5. What can you say almost the ii players' shooting accuracy and consistency?

Are you prepare for more?

Invent a data gear up with a hateful of seven and a MAD of 1.

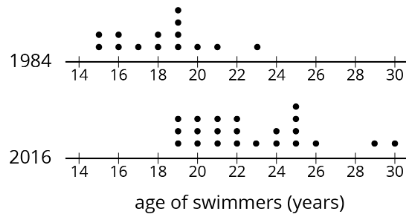
Practice \(\PageIndex{3}\): Swimmers Over the Years

In 1984, the mean age of swimmers on the U.Southward. women's swimming team was 18.ii years and the MAD was 2.ii years. In 2016, the mean historic period of the swimmers was 22.8 years, and the MAD was three years.

1. How has the boilerplate age of the women on the U.Due south. pond squad changed from 1984 to 2016? Explain your reasoning.
2. Are the swimmers on the 1984 team closer in age to one another than the swimmers on the 2016 team are to i another? Explain your reasoning.
3. Here are dot plots showing the ages of the women on the U.S. swimming squad in 1984 and in 2016. Apply them to make two other comments about how the women's swimming team has changed over the years.

Effigy \(\PageIndex{2}\): Two dot plots, age of swimmers in years, 14 to xxx by twos. First plot labeled 1984, commencement with fifteen in increments of i, the number of dots above each increment is ii, 2, 1, 2, iv, 1, 1, 0, 1. Second plot labeled 2016, starting time with 19 increments of 1, the number of dots higher up each increment is 3, 3, iii, three, 1, 2, 4, ane, 0, 0, ane, 1.

Summary

Sometimes two distributions have different means just the same MAD.

Pugs and beagles are two different dog breeds. The dot plot shows ii sets of weight data—one for pugs and the other for beagles.

Figure \(\PageIndex{three}\): A dot plot for two sets of data: "pug weights in kilograms" and "beagle weights in kilograms". The numbers 6 through 11 are indicated and there are tick marks midway between each indicated number. There are too two triangles indicated. The offset triangle is at 7 kilograms with a horizontal line drawn below the triangle that begins at 6.5 and ends at 7.5 kilograms. The second triangle is indicated at x kilograms with a horizontal line drawn below the triangle that begins at nine.5 and ends at ten.5 kilograms. The information for "pug weights in kilograms" are equally follows: six kilograms, 1 dot. 6.2 kilograms, 2 dots. half dozen.4 kilograms, 2 dots. six.six kilograms, ii dots. 6.eight kilograms, 2 dots. 7 kilograms, iii dots. 7.two kilograms, 3 dots. 7.4 kilograms, ane dot. 7.6 kilograms, 2 dots. 7.8 kilograms, one dot. 8 kilograms, one dot. The data for "beagle weights in kilograms" are as follows: 9 kilograms, 1 x. 9.two kilograms, 2 x's. ix.four kilograms, 1 x. 9.6 kilograms, 3 x's. 9.8 kilograms, 1 10. 10 kilograms, 3 10's. 10.two kilograms, iii x's. 10.4 kilograms, 1 ten. 10.6 kilograms, ii x'due south. x.8 kilograms, 2 x's. 11 kilograms, 1 x.

• The mean weight for pugs is vii kilograms, and the MAD is 0.v kilogram.
• The mean weight for beagles is x kilograms, and the MAD is 0.v kilogram.

We tin can say that, in full general, the beagles are heavier than the pugs. A typical weight for the beagles in this group is well-nigh 3 kilograms heavier than a typical weight for the pugs.

The variability of pug weights, all the same, is well-nigh the same as the variability of beagle weights. In other words, the weights of pugs and the weights of beagles are equally spread out.

Glossary Entries

Definition: Average

The boilerplate is some other proper name for the mean of a data set.

For the data set three, 5, 6, 8, xi, 12, the average is 7.5.

\(3+5+6+8+11+12=45\)

\(45\div 6=vii.5\)

Definition: Mean

The hateful is one fashion to measure the eye of a data set. We can think of it as a balance point. For example, for the data set seven, 9, 12, 13, fourteen, the hateful is eleven.

Figure \(\PageIndex{4}\)

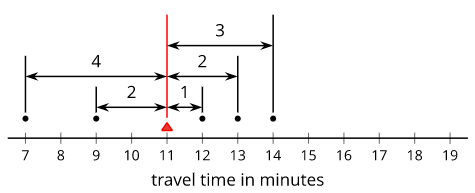
To notice the mean, add together upwards all the numbers in the data prepare. Then, divide by how many numbers at that place are. \(7+9+12+13+14=55\) and \(55\div v=11\).

Definition: Hateful Absolute Divergence (MAD)

The hateful absolute deviation is 1 style to measure how spread out a data set is. Sometimes nosotros telephone call this the MAD. For case, for the information set vii, ix, 12, 13, 14, the MAD is 2.4. This tells u.s. that these travel times are typically 2.four minutes abroad from the mean, which is 11.

Figure \(\PageIndex{5}\)

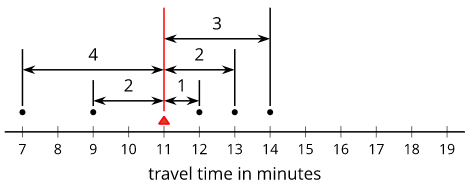
To find the MAD, add together up the distance between each data indicate and the mean. So, separate by how many numbers there are.

\(4+2+i+2+3=12\) and \(12\div 5=2.4\)

Definition: Measure of Center

A measure out of eye is a value that seems typical for a information distribution.

Hateful and median are both measures of heart.

Practise

Exercise \(\PageIndex{4}\)

The dot plots show the amounts of time that x U.Due south. students and ten Australian students took to get to school.

Figure \(\PageIndex{6}\): Ii dot plots, travel fourth dimension in minutes, 0 to sixty past tens. Kickoff plot, U S, information indicates ii minutes, 2 dots. half dozen minutes, 2 dots. vii minutes, three dots. 11 minutes, 1 dot. 17 minutes, 1 dot. 20 minutes, i dot. Second plot, Australia, data indicates 5 minutes, 1 dot. vii minutes, 1 dot. 9 minutes, 1 dot. xv minutes, 2 dots. twenty minutes, 3 dots. 25 minutes, 1 dot. 45 minutes, ane dot.

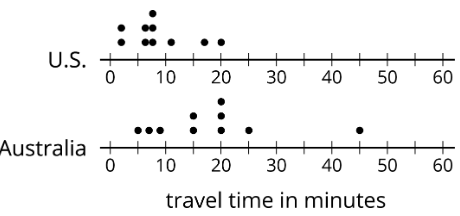
Which argument is true about the MAD of the Australian information set?

1. Information technology is significantly less than the MAD of the U.Due south. data set.
2. It is exactly equal to the MAD of the U.S. information set.
3. It is approximately equal to the MAD of the U.Due south. data prepare.
4. It is significantly greater than the MAD of the U.Southward. information set.

Do \(\PageIndex{5}\)

The dot plots show the amounts of time that ten South African students and 10 Australian students took to get to schoolhouse. Without computing, answer the questions.

Figure \(\PageIndex{7}\): Two dot plots, travel time in minutes, 0 to sixty by tens. First plot, South Africa, data indicates 5 minutes, ii dots. 10 minutes, two dots. 15 minutes, ii dots. 30 minutes, 1 dot. xl minutes, one dot. 45 minutes, 1 dot. sixty minutes, i dot. 2d plot, Australia, data indicates v minutes, 1 dot. seven minutes, i dot. 9 minutes, one dot. fifteen minutes, 2 dots. xx minutes, iii dots. 25 minutes, one dot. 45 minutes, 1 dot.

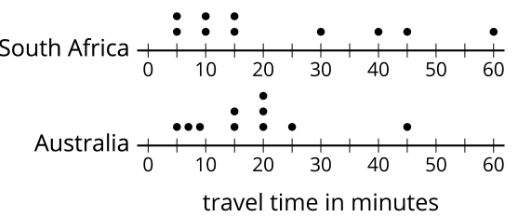
1. Which data set has the smaller mean? Explicate your reasoning.
2. Which data set has the smaller MAD? Explain your reasoning.
3. What does a smaller mean tell u.s.a. in this context?
4. What does a smaller MAD tell us in this context?

Exercise \(\PageIndex{6}\)

2 high school basketball teams have identical records of 15 wins and two losses. Sunnyside Loftier School's hateful score is fifty points and its MAD is 4 points. Shadyside High School'southward mean score is lx points and its MAD is xv points.

Lin read the records of each team's score. She likes the squad that had nearly the same score for every game it played. Which team practice you think Lin likes? Explain your reasoning.

Exercise \(\PageIndex{7}\)

Jada thinks the perimeter of this rectangle tin be represented with the expression \(a+a+b+b\). Andre thinks it can exist represented with \(2a+2b\). Exercise y'all concur with either of them? Explicate your reasoning.

Figure \(\PageIndex{8}\)

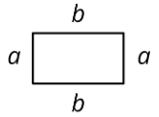
(From Unit of measurement 6.2.3)

Practice \(\PageIndex{8}\)

Draw a number line.

1. Plot and label 3 numbers between -2 and -8 (non including -2 and -eight).
2. Utilise the numbers you plotted and the symbols \(<\) and \(>\) to write iii inequality statements.

(From Unit of measurement vii.1.iii)

Exercise \(\PageIndex{9}\)

Developed elephant seals generally weigh about five,500 pounds. If you lot weighed 5 elephant seals, would you expect each seal to counterbalance exactly v,500 pounds? Explain your reasoning.

(From Unit 8.1.2)

Source: https://math.libretexts.org/Bookshelves/Arithmetic_and_Basic_Math/Book:_Basic_Math_%28Illustrative_Mathematics_-_Grade_6%29/08:_Data_Sets_and_Distributions/8.03:_New_Page/8.3.4:_Using_Mean_and_MAD_to_Make_Comparisons

Posted by: coatesperis1986.blogspot.com

Share this post